Heuristikmodellering

Heuristikken er baseret på simulated annealing, hvilket stammer fra metalindustrien, hvor metal opvarmes til en bestemt temperatur og nedkøles ifølge et bestemt køleskema. Ved nedkøling ændres strukturen i metallet, og afhængig af kølingsraten kan forskellige egenskaber opnås (se Winston et al., 2003, s. 805). I Modellen antages at der er en initial valid løsning til rådighed. Rutenetværket opvarmes derefter til en initial temperatur, hvorefter kunder udskiftes ved hjælp af systematisk tilfældighed i forskellige etablerede ruter. Den systematiske tilfældighed styres ved hjælp af den pågældende temperatur, som pejler løsningsprocessen i en bestemt kontrolleret retning. I hver gentagelse findes en ny løsning som accepteres med sandsynligheden 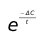, hvor ΔC er ændringen i omkostningerne for løsningen fra sidste gentagelse, og t er den nuværende temperatur. Ved accept af løsninger som ikke er bedre end den foregående løsning, forsøger heuristikken at undgå lokale optimumspunkter. Heuristikken gentages indtil løsningsprocessen fryses fast ved sluttemperaturen, idet temperaturen falder gradvist efter et bestemt antal gentagelser.

DARP er et kompliceret problem, fordi der både skal tages højde for tildeling af kunder til hver rute, og bestemmelse af i hvilken rækkefølge kunderne skal besøges. For at mindske kompleksiteten i denne proces, er der udviklet forskellige velfungerende metoder, til løsning af problemstillingen. Den klassiske metode er opdeling af  løsningsprocessen i to faser. Den første fase er gruppering af kunderne i bundter, hvorefter anden fase sørger for kunderækkefølgen i ruten (se Bergvinsdottir, 2004, s. 39, Chan, 2004, s. 16, Baugh et al. s. 102). Hver kunde kan kun være en del af et bundt, og der kan ikke være mere end en vogn om hvert kundebundt. Simulated annealing kan derefter anvendes til den første fase i løsningsprocessen, da det afgørende for løsningskvaliteten er en fordeling af kunderne i så gode bundter som muligt (se Baugh, et al., 1998, s. 103). Fase to, hvor rutelægningen udføres, kan heuristikken "The modified space-time heuristic algorithm" anvendes (se Bergvinsdottir et al., 2004, s. 10). Denne heuristik er forholdsvis hurtig og kan generere meget gode løsninger, fordi kundebundternes størrelse sandsynligvis er begrænsede i størrelsesordenen 10-20 kunder (se Baugh et al., 1998, s. 103). En variation af denne fremgangsmåde er dannelse af kundebundter, som allerede bestemmer ruterækkefølgen, hvorefter et forskydningsprincip kan anvendes til minimering af ventetid i ruten (se Cordeau et al., 2003, s. 587 og Mauri et al. 2006 s. 6). Ifølge Bergvinsdottir (2004, s. 100), er "The modified space-time heuristic algorithm" for langsom i forhold til metoden anvendt af Cordeau et al. (2003), da relativt færre gentagelser kan udføres på tilsvarende hardware på samme tid. Forskellen er så stor, at skylden sandsynligvis ikke kan lægges på hverken programmeringssprog eller rutiner.

Kvaliteten af løsningerne afhænger i høj grad af antallet af gentagelser en metaheuristik foretager under en modelkørsel, hvorfor forskydningsprincippet vælges til løsning af problemstillingen i fase to.

Kilder