Den initiale model vil være en simpel udgave i forhold til avancerede modeller set i litteraturen. Grunden til denne fremgangsmåde er, at modellen forsøges løst til optimalitet, selvom problemet er formuleret som et MILP problem. Problemet indeholder også variabler, der begrænses til heltalsværdier. Heltalsbegrænsningen vil sandsynligvis øge sværhedsgraden og derved løsningstiden for problemet (se Winston et al., 2003, s. 475).
I litteraturen bruges generelt samme notation til modelformuleringen med få afvigelser til opbygning af objektfunktion. I denne opgave er den matematiske modelformulering hovedsageligt baseret på følgende kilder: Baugh et al. (1998, s. 93), Bergvinsdottir (2004, s. 21) og Jørgensen (2002, s. 69).
Valg af modelformat
Baugh et al. (1998, s. 99) gennemgår forskellige fremgangsmåder til opbygning af den matematiske MILP model. Den største forskel mellem modellerne er antallet af binære variabler i forhold til antallet af begrænsninger. Disse to parametre kan bruges til estimering af problemstillingens sværhedsgrad og herved løsningstiden. Ingen af ovenstående modelbeskrivelser er signifikant bedre end andre, hvorfor den generelle modelformulering fra de førnævnte kilder anvendes til den matematiske modelopstilling.
Modelbeskrivelse
Modellens notation og formulering er udarbejdet, så modellens dynamik sikres, hvorved ændringer i antal vogne og kunder kan foretages uden problemer. Funktionalitet af modellen bliver undersøgt på en enkelt kunde og en enkelt vogn. Derefter bliver modellen afprøvet med flere kunder og vogne for at undersøge, om løsningstiderne er acceptable på tilgængeligt hardware og software.
Modellen optimeres efter en objektfunktion, som definerer problemstillingens omkostninger, der skal minimeres. Det svære ved DARP er problemets objektfunktion, der består af modstridende mål. Optimeringen foregår generelt på baggrund af omkostninger baseret på kvaliteten af kundeservice, transportomkostningerne og antallet af vogne anvendt i løsningen. I testversionen af modellen skal objektfunktionen være så simpel som muligt, hvorfor en minimering af antallet af kanter anvendt i løsningen udføres.
Ruterne skal lægges korrekt, og forskellige tidsfaktorer skal overholdes, hvorfor en række begrænsninger opstilles. Disse begrænsninger sørger for, at alle vogne, som forlader deres depot, kommer hjem igen. Alle kunderne skal afhentes på deres afhentningspunkter og afleveres på deres afleveringspunkter indenfor bestemte tidsperioder. En kunde skal kun besøges af en vogn og skal afhentes, før aflevering kan finde sted. Modellen understøtter ikke, at en kunde bliver afhentet af en vogn og afleveret af en anden, hvilket også ville medføre en udvidelse af problemets kompleksitet på grund af flere mulige løsningspar. Begrænsninger, der sørger for, at tidsfaktoren bliver overholdt, er vigtige parametre for kundeservicen. Kunderne skal afhentes og afleveres indenfor specificerede tidsvinduer, hvis bredde kan have betydning for opnåelse af besparelser i transportomkostningerne. Sandsynligheden for besparelser er positivt afhængig af tidsvinduernes bredde. Ulempen ved brede tidsvinduer er, at det går ud over kundernes serviceniveau. Kundernes servicenedsættelse skyldes, at en kunde risikerer afhentning lang tid før eller efter det aftalte afhentningstidspunkt og aflevering på et tidligere tidspunkt end krævet. For at sikre kundens serviceniveau er acceptabelt, anvendes maksimal turlængde MRT (Maksimum Ride Time). Det er en faktor, som har indflydelse på, hvordan tidsvinduerne kan opbygges. En MRT, der svarer til halvanden gange den direkte transporttid, anvendes. En længere MRT giver mulighed for transport af flere kunder i samme rute med risiko for lang transporttid.
Modelnotation
Modellen afspejler en problemstilling med n antal kunder og v antal vogne. Disse kunder og vogne tildeles ID-numre ved hjælp af prædefinerede sæt. Depoterne er oplistede først, hvorefter kundernes afhentnings- og afleveringspunkter defineres. Startdepoterne defineres fra 1,...,v, slutdepoterne v+1,...,2v, afhentningspunkterne 2v+1,...,2v+n og endeligt afleveringspunkterne 2v+n+1,...,2v+2n. Følgende sæt bliver anvendt i modelopbygningen.
V = {1,...,v} Vogne, som svarer til til startdepoterne.
Do = {1,...,v} Startdepoter.
Dd = { v+1,...,2v} Slutdepoter.
P = {2v+1,...,2v+n} Afhentningspunkter.
D = {2v+n+1,...,2v+2n} Afleveringspunkter.
N = P U D Afhentnings- og afleveringspunkter.
A = N U Do U Dd Alle knudepunkter.
Udover ovenstående sæt defineres parametre, som er konstante værdier, der anvendes af problemløseren som rå data. Parametrene indeholder information om servicetid, lastændring, kapacitet i vognene, start- og sluttid på tidsvinduer. Endvidere defineres M, som er en stor positiv værdi, der anvendes i forbindelse med linearisering af begrænsninger. Det kritiske punkt for M-værdien findes ved beregning af antallet af minutter i planlægningsperioden, som er et døgn (24 · 60 = 1440 minutter). Det antages, at et knudepunkt ikke forlades af en vogn senere end planlægningsperiodens sluttidspunkt. En liste over anvendte parametre er vist herunder.
v antal tilgængelige vogne.
n antal kunder.
si servicetid i punkt i.
li lastændring ved knudepunkt i.
Ci kapacitet i vogn i.
ai tidsvindue starttid i knudepunkt i.
bi tidsvindue sluttid i knudepunkt i.
M M stor positiv værdi.
Beslutningsvariabler er de værdier, som kan ændres af problemløseren i løbet af optimeringsprocessen. De anvendes til bestemmelse af, hvorvidt en vogn skal køre på en bestemt strækning, hvornår vognen forlader et bestemt knudepunkt, og hvad lasten i vognen er, når knudepunktet forlades. De tre beslutningsvariabelsæt er vist herunder.
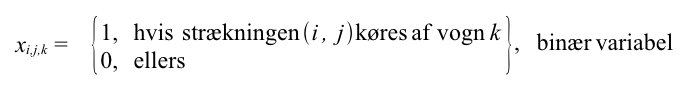
Ti,k = tidspunkt når knudepunktet i forlades af vogn k, heltallig variabel, ≥ 0.
Li,k = last når knudepunkt i forlades af vogn k, heltallig variabel, ≥ 0.
Notationen er defineret, og modellen kan opbygges med objektfunktion og begrænsninger.
Modelformulering
I et optimeringsproblem skal en objektfunktion opstilles, som problemløseren skal minimere eller maksimere. I DARP udtrykkes objektfunktionen som en omkostningsfunktion, der skal minimeres. Til testmodellen opstilles den simple objektfunktion (9.1), der summerer alle strækninger, alle vogne kan køre. Ud fra den opstillede objektfunktion vil en vogn i den optimale løsning starte i sit depot, afhente og aflevere alle kunderne og returnere til sit depot. Vognens transportomkostninger i forhold til afstanden mellem knudepunkterne er ikke medtaget her.

Begrænsning (9.2) sørger for, at alle tilgængelige vogne kører ud til et afhentningspunkt. Der summeres over alle afhentningspunkter samt slutdepoter, hvorved vogne, som ikke anvendes, kan køre direkte fra start- til slutdepot. Denne begrænsning er nødvendig, så hver vogn ikke forlader depotet mere end én gang.

Den næste begrænsning (9.3) sørger for, at alle vogne, der har forladt deres depot, returnerer til deres slutdepot.

Begrænsning (9.4) er nødvendig, fordi den sikrer, at hver kunde kun bliver afhentet en gang, hvorefter vognen kører til et afleveringspunkt.
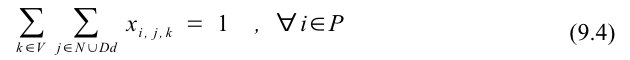
Begrænsningen (9.5) sørger for, at den vogn, som afhenter en bestemt kunde, også afleverer kunden i afleveringspunktet.
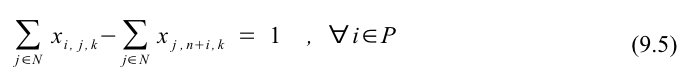
Besøges punkt j efter punkt i skal punkt i besøges tidsmæssigt før punkt j, som begrænsning (9.6) sørger for. Tiden, når vognen besøger punkt i plus servicetiden i punkt i, skal være mindre end eller lig tiden, når vognen er i punkt j. Begrænsningens ulighed er altid opfyldt, hvis en vogn ikke kører mellem knudepunkt i og j, da parameteren M i tilfældet sørger for en negativ venstreside.
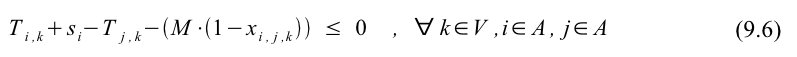
I tilfælde hvor punkt i besøges af en vogn, skal vognen være i punktet indenfor tidsperioden defineret af punktets tidsvindue. Tidsvinduet angives med et start- og sluttidspunkt defineret af henholdsvis parametrene ai og bi. Begrænsning (9.7) sørger for overholdelse af tidsvinduerne for alle knudepunkter. Tidsvinduer for start- og slutdepoterne kan også defineres og anvendes til begrænsning af en vogns anvendelsesperiode i en given planlægningsperiode.
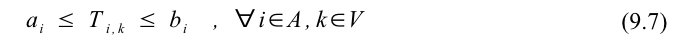
Afhentning af en kunde skal ske tidsmæssigt før kunden afleveres, hvorfor begrænsning ( 9.8 ) er anvendt.
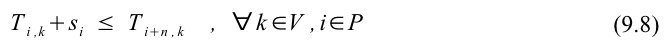
Begrænsning (9.9) sørger for, at kapaciteten, der bruges af en kunde i et afhentningspunkt, er lig kapaciteten, der frigøres ved afleveringspunktet. Det antages her, at hvis en kørestolsbruger og kørestol afhentes, vil både kunden og kørestolen afleveres i afleveringspunktet. Begrænsning (9.9) er ikke lineær, men lineariseres efter samme princip som begrænsning (9.6), hvilket resulterer i de to lineære begrænsninger (9.10) og (9.11).
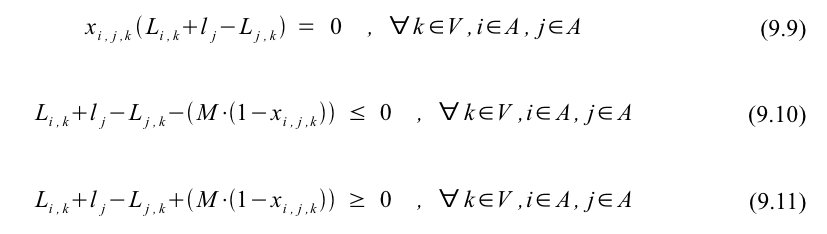
Vognkapaciteten skal overholdes, hvorfor lasten undersøges i alle punkter, en vogn besøger. Når punkt i forlades, skal lasten altid være større eller lig lastændringen i punktet og være mindre end eller lig vognkapaciteten. Alle vognkapaciteterne i alle punkter overholdes på grund af begrænsning (9.12).
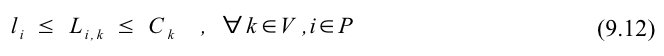
Alle vogne skal starte og slutte tomme, hvilket er udtrykt i nedenstående begrænsningssæt (9.13).
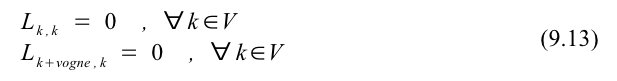
Ovenstående begrænsningssæt fra 9.2 til 9.13 definerer den endelige testmodel. Modellen er vist i sammenhæng herunder og afprøves med forskellige antal kunder og vogne.

Modelafprøvning
Til modelafprøvningen er anvendt forskellige løsningsværktøjer for at udelukke fejl, der kan være forskyldt af løsningsværktøjet. Værktøjerne GLPSOL (GNU Linear programming solver)1, LP løseren SoPlex (The Sequential object-oriented simPlex)2 der anvendes af MILP løseren SCIP (Solving Constraint Integer Programs)3, og endeligt er NEOS serveren anvendt i forbindelse med SCIP og CPLEX4. GLPSOL er frit software, som kan anvendes frit af alle. SoPlex og SCIP må kun anvendes frit i forbindelse med forskning, mens CPLEX er en state of the art kommerciel LP løser.
Til selve modelleringen anvendes GNU mathprog modeling language, som er frit matematisk modelleringssprog, der svarer til AMPL (A Modeling Language for Mathematical Programming)5, som er en kommerciel ækvivalent. GNU mathprog følger med i samme softwarepakke som GLPSOL, hvorfor GNU mathprog kan aflæses direkte af GLPSOL. Modelfilerne kan derefter konverteres til MPS format, der kan læses af SCIP og NEOS. I tilfælde hvor GLPSOL ikke er i stand til at finde en løsning, kan SCIP og NEOS afprøves.
Det første forsøg er baseret på en vogn og en kunde, der består af fire knudepunkter 1-4, som er henholdsvis vognens startdepot, vognens slutdepot, kundens afhentnings- og afleveringspunkt. Den forventede løsning har derfor følgende rutesekvens 1-3-4-2 (startdepot-afhentningspunkt-afleveringspunkt-slutdepot se figur 9.1). En kørsel af modellen test00.mod genererer en optimal løsning med to ruter i stedet for den forventede ene rute. I den første rute i løsningen kører vognen fra sit startdepot til slutdepot (1-2), og i den anden rute kører vognen fra kundens afhentningspunkt til kundens afleveringspunkt (3-4). Denne løsning medfører en objektfunktionsværdi, som er minimeret til 2 (x variabler med værdien 1: x121 og x341). Dette er ikke en valid løsning, da vognen i rute nummer to hverken starter eller slutter i sit depot. Denne testmodel er baseret på en basismodel (se Jørgensen, 2002, s. 73), som sandsynligvis er mangelfuld. Der mangler en begrænsning, der sørger for, at alle afhentnings- og afleveringspunkter forlades igen, hvis de besøges af en vogn. Begrænsningen skal tvinge vognen til at forlade afleveringspunktet i knudepunkt 4 i ruten 3-4. Vognen tvinges derfor til kørsel på strækningen j,i, når der køres på strækningen i,j. Dette gælder for alle punkter i problemet j og alle afhentnings- og afleveringspunkter i. Begrænsningen kan udtrykkes ved hjælp af følgende matematiske udtryk (9.14) (se Baugh et al., 1998, s. 94 og Bergvinsdottir, 2004, s. 22).
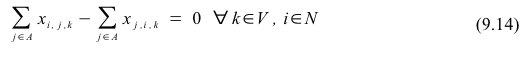
Denne begrænsning sørger for aktivering af strækningen (j, i) = (én af alle knudepunkter, 3), når en vogn færdes på strækningen (i, j) = (3, 4). Vognen skal derfor køre på en strækning, der lander i knudepunkt 3. Endvidere tvinges vognen tilbage til sit depot af begrænsning (9.3), hvorfor knudepunkt 2 også besøges. Ved tilføjelse af ovenstående begrænsningssæt til modelformuleringen dannes model test01.mod, som kan løses til optimalitet og giver følgende forventede og valide rute 1-3-4-2 med en objektfunktionsværdi på 3. Følgende x variabler er aktiveret (x131 , x341 og x421). Løsningerne kan findes i output.txt filerne på DVD'en i samme sti som modelfilerne (DVD/MILP/).
Målet er, at få modellen til at løse problemer med 1000+ kunder og 500+ vogne. Testdata er nødvendige til opstilling af et testscenarie, som skal afspejle problemstillingens parametre med forskellige antal kunder og vogne. Til formålet er en en parametergenerator7 opbygget, der generer tilfældige data. Modellerne test02.mod og test03.mod er kørt med henholdsvis (kunder, vogne) = (n, v) = (5,5); (10, 10); (100, 100). Den mindste model på (n, v) = (5, 5) løses med alle værktøjerne på under et minut. GLPSOL kan ikke løse en modelstørrelse på (n, v) = (10, 10) indenfor to timer, mens SCIP/SOPLEX finder den optimale løsning i løbet af 59 minutter og SCIP/CPLEX i løbet af 13 minutter. Modellen med (n, v) = (100, 100) medfører hukommelsesmangel, selvom den tilgængelige hukommelse er på to GB RAM. Flere testforsøg udføres ikke, da det antages, at forbedringer i modellen ikke kan mindske hukommelsesforbruget betydeligt.
Med det tilgængelige hardware har det vist sig, at optimal matematisk løsning af problemet i nødvendig størrelsesorden ikke er mulig. Mere hukommelse vil ikke løse problemet, da løsningstiden stiger betydeligt, når flere kunder og vogne tilføres problemet. En afgørende faktor er derfor også processor kraften, som ikke er tilstrækkelig i nutidens computerhardware. På baggrund af forgående forsøg, vil det videre arbejde til løsning af problemstillingen koncentreres om andre løsningsmetoder.
Kilder