DARP er blevet behandlet i litteraturen siden 1970'erne, hvor de første heuristikker blev udviklet til løsning af DARP, og interessen steg yderligere i starten 1980'erne (se Psaraftis, 1983, s. 133). Årsagen til den stigende interesse var sandsynligvis udviklingen og tilgængeligheden af IT, der kunne anvendes til løsning af DARP. I begyndelsen fik det statiske DARP mest opmærksomhed på grund af de lempede krav til løsningstiden i forhold til det dynamiske DARP. Litteraturen præsenterer robuste løsningsmodeller til både den statiske og dynamiske del. Der er ikke klar enighed om, hvilken metode der er bedst i forskellige praktiske tilfælde. En af grundene til uenigheden er sandsynligvis, at vægtningen af optimeringsfunktionen er unik og situationsbestemt i forskellige praktiske tilfælde.
Dynamisk DARP
Brandvæsenet i København fik hjælp af Madsen et al. (1995, s. 193) til løsning af deres DARP, som indeholdte 50.000 kundeordrer om året. Kundeordrerne bestod mest af transport af ældre og handicappede. Den anvendte heuristik er en indsættelsesalgoritme kaldet REBUS, som er baseret på en multikriterie objektfunktion, der tager højde for kundeservice og transportomkostninger. Indsættelsesalgoritmen er af typisk karakter for grådige heuristikker, hvor alle ordrer som ikke er rutelagt bliver indsat i det eksisterende rutenetværk en af gangen. Alle mulige indsættelseskombinationer for ordren i alle ruter bliver undersøgt, og ændringen i objektfunktionen beregnes hver gang. Ordren indsættes i den ruteposition, som er billigst i forhold til objektfunktionen. En ordre kan ikke altid serviceres af de eksisterende vogne, hvorfor den lægges i listen med ordrer, der ikke kan opfyldes. Alle ikke opfyldte ordrer kan derefter blive serviceret af tredjepart eller afvises helt. Hele proceduren er en sekventiel proces, som stopper, når aller kundeordrerne er tildelt en vogn eller er i listen over ordrer, der ikke kan opfyldes. Fordelen ved REBUS i forhold til en traditionel indsættelsesheuristik er, at kundeordrer som endnu ikke er rutelagt, sorteres i forhold til, hvor svære de er at indsætte. Endvidere præsenterer REBUS nye muligheder indenfor objektfunktionsopbygningen, og optimeringen tager højde for flere vognkapacitetsbegrænsninger. Ovenstående egenskaber viser indsættelsesheuristikkens fordele i forhold til en simpel indsættelsesmetode.
Jørgensen (2002) implementerer systemet Inforoute, der kan løse DARP hos Jensen Turisttrafik, som er en busoperatør. Systemet anvender en indsættelsesheuristik, der minder om den anvendte i REBUS. Det specielle ved implementeringen af Inforoute er metoden til lægning af den initiale løsning. Den initiale løsning kan lægges før dagens start, fordi nogle af kundeordrerne er kendt dagen før. Den anvendte algoritme til den initiale løsning er baseret på klyngedannelse (se Jørgensen, 2002, s. 154). Ved hver kundeindsættelse, undersøges om der er en eksisterende klynge, som kunden kan være en del af. En ny klynge dannes, hvis kunden ikke kan placeres i en eksisterende klynge. Klyngedannelsen er kun baseret på den første kunde i klyngen, hvorfor klyngestørrelserne begrænses. Tanken bag metoden til klyngedannelse er, at en god initial løsning kan være fordelagtig, så den grådige indsættelsesheuristik har et godt udgangspunkt. Klyngedannelsen er mere tidskrævende end den grådige indsættelsesheuristik, men tidsfaktoren er ikke et problem, fordi den initiale løsning kan lægges om aftenen dagen før.
I landområdet omkring Los Angeles har Diana et al. (2004) undersøgt en ny indsættelsesheuristik til løsning af DARP. Indsættelsesrækkefølgen af kundeordrer er sorteret efter et nyt princip, der forsøger at indsætte kundeordrer, som ved senere indsættelse sandsynligvis vil kræve højere omkostninger. Sorteringsprincippet er baseret på den geografiske tæthed af kundernes afhentnings- og afleveringspunkter. En kunde i et område med lav efterspørgsel er derfor sværere at indsætte. Derefter anvendes en parallel indsættelsesalgoritme baseret på fortrydelse. Omkostningerne for alle kunders indsættelsesmuligheder beregnes, hvorefter den kunde indsættes, som er dyrest ikke at indsætte. Systemet vælger derfor en kunde der minimerer sandsynligheden for høje omkostninger, så systemets handlinger ikke fortrydes senere i forløbet. Indsættelsen er baseret på omkostningsberegninger, der på tidspunktet er tilgængelige. Informationerne ændrer sig fra gentagelse til gentagelse, hvorfor en indsættelse på et bestemt tidspunkt ikke sikrer global optimalitet.
En heuristik der tager højde for to tidshorisonter, den korte – og lange tidshorisont er blevet udviklet af Mitrovic-Minic et al. (2004). Disse tidshorisonter er implementeret i objektfunktionen, hvorved indsættelsesheuristikken kan tage højde for kunder, der skal transporteres på forskellige tidspunkter af dagen. Under kundeindsættelsen i starten af dagen kan der tages højde for efterspørgslen senere på dagen. Denne strategi kan muliggøre generering af bedre løsninger. Opnåede besparrelser ved hjælp af denne fremgangsmåde er faldende, når problemstørrelsen stiger. Den største undersøgte problemstørrelse er på 1000 kunder.
Statisk DARP
En accepteret metodegruppe til løsning af det moderne statiske DARP med realistiske begrænsninger er metaheuristikker. Disse heuristikker er tidskrævende og løsningernes kvalitet er stærkt afhængig af heuristikkens kørselstid (se Mitrovic-Minic et al., 2004, s. 672). Fordelen ved disse heuristikker er, at de ikke er afhængige af hverken sekventiel eller parallel indsættelsesrækkefølge, hvorfor sandsynligheden for optimale eller nær optimale løsninger stiger.
Baugh et al. (1998) anvender en fremgangsmåde der starter med klyngedannelse og rutelægger til sidst. Klyngedannelsen er baseret på en simulated annealing heuristik, hvor simple tilfældige ændringer i løsningen foretages. Et køleskema anvendes, som sørger for kontrolleret søgning i løsningsmængden og afslutning af heuristikken i løbet af rimelig tid. Ændring af løsningen foretages på baggrund af to forskellige ændringsoperationer. Den første ændringsoperation bytter to kunder fra to forskellige ruter ud med hinanden. Den anden ændringsoperation flytter en tilfældig kunde fra sin rute til en anden tilfældig rute, som kan være en helt ny rute. Problemet relakseres ved søgning i løsningsmængder der er værre end den hidtil bedste løsning. Dette opnås ved accept af omkostningsforværrende ændringsoperationer med en hvis sandsynlighed. Risiko for søgning i løsningsmængden der går i ring og derved fanges i et lokalt minimum mindskes ved anvendelse af en simpel tabuliste. Ændringer i løsningen forbydes, hvis de anvender kunder fra tabulisten.
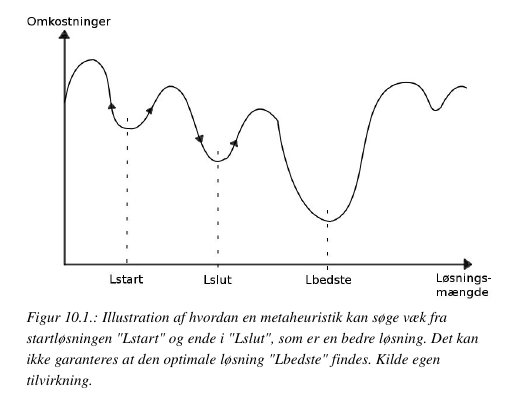
Figur 10.1 viser hvordan en metaheuristik forsøger at søge væk fra et lokalt minimum. Heuristikken starter i løsning Lstart, som er fanget i et lokalt minimum. En søgning i løsningsmængden med højere omkostninger medfører en ny løsning Lslut. Denne løsning er bedre end Lstart, men er også fanget i et lokalt minimum. Det globale optimum Lbedste findes ikke, hvilket ikke er atypisk, da heuristikker ikke kan garantere globalt optimale resultater.
En metaheuristik baseret på tabusøgning er udviklet af Cordeau et al. (2003), og har vist sig at være en stabil og intelligent løsningsmetode. Grundlæggende minder metoden om simulated annealing udviklet af Baugh et al. (1998). Fremgangsmåden er anderledes, da en tabuliste anvendes i stedet for et køleskema som det primære konvergeringsværktøj. Metoden udvides med en tredje ændringsoperation til ændring af løsningen, der bytter to kunder i samme rute ud med hinanden. Tabusøgningsmetoden anvender den bedste indsættelse af en kunde, når en kunde flyttes fra en rute til en anden i stedet for tilfældige ryk som i simulated annealing. Beregning af kundens bedste indsættelsesposition er en tidskrævende procedure, men kan resultere i bedre resultater, selvom indsættelsesmetoden er grådig. Anvendelsen af tabusøgning til løsning af DARP har vist sig at være fordelagtig, fordi gode løsninger kan findes selv efter få gentagelser (se Chan, 2004, s. 63). Grunden til de gode resultater er sandsynligvis minimeringen af tilfældighed og anvendelse af tabulistens hukommelse.
Bergvinsdottir (2004) og Bergvinsdottir et al. (2004) arbejder på en relativ ny metode til løsning af DARP baseret på genetiske algoritmer. I stedet for klyngedannelsen ved hjælp af simple tilfældige ændringsoperationer, baseres løsningsændringer på parringer mellem løsningssæt. Det bedste afkom fra disse parringer erstatter løsninger med høje omkostninger. En anden metode til ændring af løsningerne er ved hjælp af krydsning af to tilfældige ruter fra to forskellige løsninger. Dette danner en skabelon til en ny rute, som ifølge et regelsæt, tager de nødvendige informationer fra de to ruter og laver en ny rute. I tilfælde af at den nye løsning ikke er valid, allokeres eller frasorteres kunder fra tilfældige ruter. Mutation kan også anvendes til ændring af løsningen, hvor en tilfældig kunde flyttes fra sin rute til en anden tilfældig rute. De endelige løsninger, som genetiske algoritmer kan generere, kan sammenlignes med heuristikken baseret på tabu søgning udviklet af Cordeau et al. (2003). Ulempen ved den genetiske algoritme er den forholdsvist store mængde beregninger med basis i tilfældighed, som gør anvendelsen langsom. Ekstraordinære lange løsningstider kan også opstå, når problemer med mange kunder skal løses (se Bergvinsdottir et al., 2004, s. 10).
En kombination af rutelægningsprincipperne fra Cordeau et al. (2003) og en diversifikationsstrategi baseret på simulated annealing (se Baugh et al., 1998) er udviklet af Mauri et al. (2006). Den nye heuristikopbygning er forholdsvis hurtig på baggrund af den simple struktur, der blandt andet ikke indeholder en tabuliste og minimerer beregningsmængden. Ifølge Mauri et al. (2006, s. 10-11) er deres simulated annealing heuristik bedre end den genetiske algoritme præsenteret af Bergvinsdottir et al. (2004) på alle målte kriterier: samlet rutetid, ventetid, køretid og CPU tid til generering af løsningen. Cordeau et al. (2003) heuristikken er signifikant bedre med hensyn til den totale køreafstand. Den nye simulated annealing heuristik præsenterer bedre resultater med hensyn til ventetid, kundekøretid og høj reduktion i CPU tid i forhold til Cordeau et al. (2003). Det største problem der anvendes til sammenligning af heuristikkernes kvalitet er en problemstørrelse på (n = 144, m = 10) (kunder, vogne), hvilket resulterer i et fald i CPU tiden fra 92,4 til 2,8 minutter til fordel for teknikken i Mauri et al. (2006) i forhold til Cordea et al. (2003).
Valg af heuristik
Valgmulighederne består af tre forskellige metaheuristikker: genetiske algoritmer, tabusøgning eller simulated annealing. En kombination af ovenstående heuristikker kan også anvendes. På baggrund af litteraturgennemgangen udvælges den bedste heuristik til problemstillingen ved hjælp af udelukkelsesmetoden.
Heuristikker baseret på genetiske algoritmer, er stadig under udviklingsfasen, hvorfor uventede problemer kan forekomme. Estimering af gode parameterværdier kan endvidere være svære på baggrund af de mange indstillingsmuligheder i den genetiske algoritme (se Bergvinsdottir, 2004, s. 76). Det er derfor sandsynligvis nødvendigt med præliminære undersøgelser for de enkelte parameterværdier hver gang et nyt problem skal løses.
Tabusøgning og den nye simulated annealing metode er de to heuristikker, der vælges imellem. Det endelige valg af heuristik, skal baseres på parametre, der er vigtige i en given problemstilling. Tidsfaktoren er vigtig, fordi problemets statiske størrelse (n = 1000+, m = 500+) ikke er behandlet i litteraturen, hvorfor en bestemt teknik ikke er åbenlys. Tabusøgning kan være et risikabelt valg, på baggrund af en løsningstid på 92,41 minutter for en problemstørrelse på (n, m) = (144, 10) (se Cordeau et al., 2003, s. 589). For at maksimere sandsynligheden for et systemet, der kan generere gode brugbare løsninger, vælges den hurtigste heuristik baseret på simulated annealing. En acceptabel løsningstid kan medføre implementering af en tabuliste til forbedring af resultaterne som i Baugh et al. (1998).
Anvendelse af simulated annealing til løsning af DARP er blevet kritiseret, fordi den velkendte løsningsstruktur gør udvikling af intelligente søgningsheuristikker fordelagtig (se Jørgensen, 2002, s. 52). Tabusøgningsheuristikken udviklet af Cordeau et al. (2003) anvender grådige heuristikker til ruteprogrammeringen, hvilket medfører en stigning i tidsforbruget, når disse beregningstunge teknikker implementeres. Det høje tidsforbrug er ufordelagtigt i forhold til den positive korrelation mellem metaheuristikkernes løsningskvalitet og afviklingstiden. Metaheuristikker med simple og beregningslette operationer, der tillader mange ændringer i løsningen i løbet af kort tid, kan derfor være fordelagtige. Simulated annealing viser hvordan mange simple ændringer i løsningen kan genere gode resultater på kort tid (se Mauri et al., 2006, s. 10).
Udover tidsfaktoren er fordelen ved simulated annealing, at heuristikken ifølge Mauri et al. (2006, s. 11) reducerer vognenes ventetid. Reduktion af ventetid med kunder er fordelagtig, hvis en øget kundeservice ønskes. Resultaterne præsenteret i Mauri et al. (2006, s. 10-11) skal tolkes varsomt, fordi der ikke tages højde for forskellen i objektfunktionerne anvendt i artiklerne. Resultattabellerne for de forskellige heuristikmetoder, har derfor en begrænset sammenlignelighed. En ændring af vægtningen af forskellige parametre i objektfunktionen kan resultere i, at nogle omkostninger minimeres mere end andre. En højere vægtningskoefficient ud for ventetiden, kan derfor resultere i bedre ventetidsresultater, mens resultatet af de andre parametre kan på forhånd være uklar. Disse observationer forklarer endvidere, hvorfor kun nogle parametre er forbedret i Mauri et al. (2006) kontra Cordeau et al. (2003).
Det endelige valg af fremgangsmåde er anvendelse af samme princip som i Jørgensen (2002). En god initial løsning skal genereres aftenen i forvejen. Denne løsning bliver derefter grundlag for det nuværende dynamiske system Planet. I modsætning til Jørgensen (2002), vil en metaheuristik baseret på simulated annealing anvendes, der sandsynligvis kan generere bedre løsninger end relativt hurtige heuristikker til klyngedannelse. Ifølge Baugh et al. (1998, s. 102) kan simulated annealing generere tæt på globalt optimale løsninger i løbet af rimelig tid. En anden grund til denne fremgangsmåde er, at metaheuristikken vil være enkel at implementere, så den kører sideløbende med den dynamiske system. Implementeringen er enkel fordi heuristikken er baseret på simple ændringer, der kan foretages hurtigt fra løsning til løsning.